J'essaie ici d'aller plus en avant dans le concept du foil rotatif, déjà présenté sur ce blog, mais juste en mode texte.
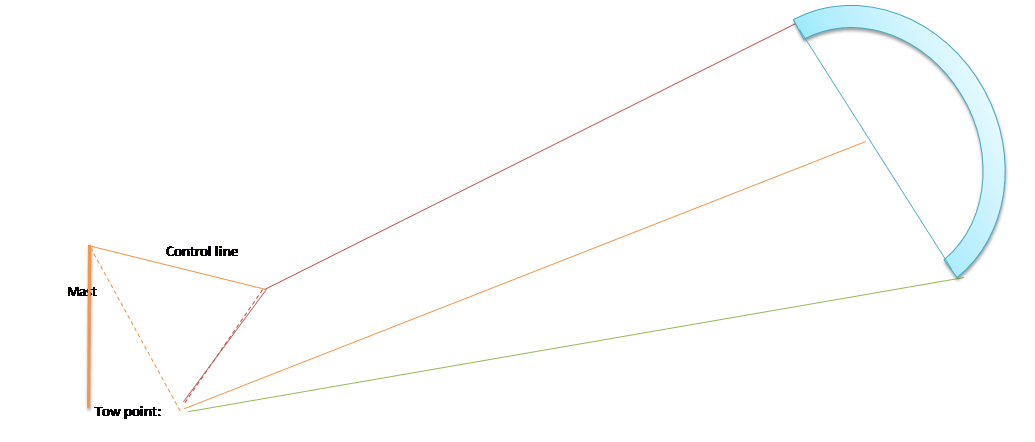
Pour commencer j'ai essayé de faire un schéma cinématique. Pour cela, j'ai de nouveau cherché les outils existant et j'ai trouvé le logiciel openmeca qui permet assez rapidement de réaliser un schéma cinématique, de l'habiller de géométrie très basique, de faire une animation cinématique ou même une simulation dynamique. Malheureusement un petit bug dans l'enregistrement du fichier de sauvegarde ne me permet pas de présenter une animation pour l'instant, mais voici une première image du concept.
Le plan marron au dessus représente une planche à voile ou un bateau.
La partie en rose représente un mât de foil vertical ("shaft" en anglais).
La partie en violet représente le foil rotatif, relié au shaft par une liaison pivot.
Le foil est excentré par rapport à l'axe de rotation grâce à un petit mât, afin de s'orienter sous l'effet de sa portance.
On considère dans un premier temps que la densité du foil est égale ou proche de celle de l'eau, ce qui revient à dire que les forces volumiques (de gravité et d'Archimède) sont négligées devant les forces hydrodynamiques.
Si l'axe de rotation est parallèle à l'écoulement, il y a une invariance par rotation et le foil étant symétrique droite/gauche, il peut être à l'équilibre dans n'importe quelle position.
Si l'on considère également que le profil du foil est symétrique et l'angle d'attaque par rapport à l'axe de rotation nul, la portance sur le foil est alors nulle. On peut s'attendre à ce que l'angle de rotation du foil soit marginalement stable (la vitesse de rotation tend vers zéro sous l'effet de la traînée et de la portance créée sur le mât, mais la position peut dériver sous l'effet de la moindre perturbation).
On considère maintenant une position initiale du foil vers le haut (le foil fait un T à l'endroit). Et l'on vient considérer l'effet d'un changement d'assiette de l'ensemble.
Si le "nez" de l'axe de rotation va vers le haut ("pitch up"), une portance sera créée sur le foil orientée vers le haut. La configuration reste symétrique, ce qui permet de dire que l'on reste à l'équilibre. Cette position d'équilibre est stable. Pour s'en convaincre, imaginons une perturbation de la position du foil à 90° vers la droite. Le mâtereau est alors à l'horizontale et le foil à la verticale. l'angle d'attaque du foil est devenu nul, mais le mâtereau a maintenant un angle d'attaque ce qui crée une portance vers le haut et un retour vers la position d'équilibre.
Si le "nez" de l'axe de rotation va vers le bas ("pitch down"), une portance vers le bas sera créée sur le foil. Mais cette fois, cet équilibre est instable. Il existe une nouvelle position d'équilibre foil tête en bas.
On voit ici que c'est le mâtereau qui donne la stabilité grâce à une double action :
- création d'un bras de levier
- portance créée par une surface transversale au foil
D'autres configurations stables sont envisageables en reprenant ces deux principes.
On peut également vouloir au contraire compenser l'effet du mâtereau en rajoutant une pièce similaire du côté opposé au foil.
On considère maintenant l'effet d'un angle de calage du foil.
Si l'on reprend le scénario ou l'axe de rotation est parallèle au flux, si on rapproche le bord de fuite de l'axe de rotation on va créer une portance vers l'extérieur. Cette portance étant tangentielle, elle ne modifie pas la symétrie et n'a pas d'effet direct sur l'équilibre ou la stabilité.
On pourrait donc de même obtenir une force tangentielle vers l'intérieur en éloignant le bord de fuite de l'axe de rotation.
Edit 2024/10/22 :
le foil n'a pas besoin d'être au bout du mâtereau, même si intuitivement cela devrait aider à la rotation.
certains m'ont fait remarquer que le tirant d'eau augmentait (à cause du mâtereau).
On peut aussi imaginer d'avoir le mâtereau un plus haut et de transmettre la rotation par un système de courroie, mais cela complexifie le système et rajoute des frottements.
To be continued.